2002-09-14 09:18 UTC Studying roads built by finite-state cellular automata
I was reading The Science of Discworld (Terry Pratchet, Ian Stewart, Jack Cohen) a couple of weeks ago when I first heard about Langton's Ant, a very simple mathematical model which demonstrates emergent behaviour. This idea intrigued me, so I implemented it to see it for myself.
The language I chose to do this was ObjectPascal (using the Free Pascal Compiler), which I learnt many years ago when I was still writing code using Delphi on Windows. ObjectPascal is a very nice language. It is clean and easy to read, and sports all the features one expects from modern languages: function and operator overloading, exceptions, class types (effectively runtime templates), runtime type information (reflection), properties with setters and getters, virtual constructors and destructors, index and string-based dynamic method dispatch, the works. The ideal language to play with Langton's Ant.
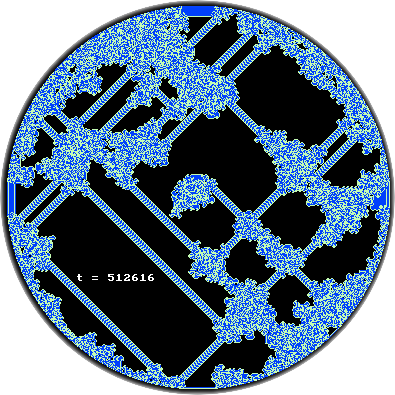
A few hours of coding later I had my first highway! (That's what Langton Ant people call the behaviour seen after ten thousand iterations.) It was a bit boring though because on modern hardware you can get to the steady state in a few milliseconds. So I added a reflective boundary to the model, and ran it again. After playing with various boundaries and playfield sizes, I settled on a circle, which showed nice behaviour. Here is a sample of the output of my program after about half a million iterations:
Watching it develop on the screen is much more fun than looking at the screenshots I made, though, so I encourage anyone who hasn't played with programs that study emergent behaviour to download the source to my program and run it yourself. (For those who want to compare notes, I wrote some descriptions of the behaviours I observed.)